1.Método de ordenamiento
Es la operación de arreglar los elementos de un determinado vector en algún orden secuencial
de acuerdo a un criterio de ordenamiento.
El propósito principal de un ordenamiento es el de facilitar las búsquedas
de los miembros del conjunto ordenado.
Al hablar de ordenación nos referimos a mostrar los datos en forma
ordenada de manera que tengan un mejor orden, ya que al momento que
el usuario ingresa los datos estos pueden ser ingresados en forma desordenada.
Metodos de Ordenacion
Ordenacion por Seleccion Ordenacion por Seleccion
Ordenacion por Insercion
Búsqueda Secuencial
Búsqueda Binaria
Metodo de Intercambio ó Burbuja
Ordenación por Selección
El proceso de la selección es el siguiente:
1)Captura el Número más pequeño (si se desea ordenar los elementos de
menor a mayor) o el número más grande (si se desea ordenar de mayor a menor).
2)El número capturado es colocado en la primera posición, teniendo en
cuenta que un Array empieza desde la posición Cero.
3)El Proceso se repite para todos los datos sobrantes hasta llegar al
último de ellos.
4)Finalmente los datos quedan ordenados ya sea en forma ascendente o
descendente..
Ordenación por Inserción
El método de ordenación por inserción es similar al proceso típico de
ordenar tarjetas de nombres (cartas de una baraja) por orden alfabético
, que consiste en insertar un nombre en su posición correcta dentro de una
lista o archivo que ya está ordenado. Cada elemento a insertar es considerado uno a la vez,
asimismo se insertan en su posición correspondiente.
Búsqueda Secuencial
Consiste en ingresar un dato a buscar, por lo cual el programa examina cada uno de los elementos del vector.
es decir, el elemento a buscar es comparado con cada uno de
los elementos que contiene el Array.
Si el Array tiene 100 elementos y el dato a Buscar esta en la
posicion 100, entonces se realizara 100 comparaciones puesto que conparará hasta llegar al final del Array,
sin embargo existe la posivilidad que el elemento a buscar
no pertenesca al Array, y la busqueda sera en vano
Búsqueda Binaria
Para poder ejecutar el Método de Búsqueda Binaria, se debe de contar con un Array ordenado. El procedimiento que se realiza es el siguiente:
•EL Programa internamente selecciona el elemento central del Array.
•Si el elemento a buscar es el dato central el proceso termina. •Si el elemento a buscar no coincide con el elemento central, continua la búsqueda:
•Se subdivide en dos partes al Array.
•Si el elemento a buscar es menor que el dato central, entonces selecciona la mitad de la parte izquierda.
•La parte seleccionada se subdivide nuevamente y se repite todo el proceso.
•El proceso termina cuando el dato es encontrado; teniendo en cuenta que el dato a buscar no puede encontrarse en el Array.
Método de Intercambio Ó Burbuja
El método de la Burbuja es menos eficiente puesto que realiza las pasadas necesarias en un array hasta que el Array quede ordenado. Su forma de ejecución es:
•En la primera pasada compara el primer elemento con el segundo elemento.
•En la misma pasada compara el segundo elemento con el tercer elemento.
•Se repite el mismo procedimiento hasta llegar al último elemento.
•Si una vez finalizada la primera pasada el Array sigue desordenado, entonces se realiza una segunda pasada.
•Se realiza el mismo procedimiento en la segunda pasada.
•Se repiten las pasadas necesarias hasta que el Array quede completamente ordenado.
Ejemplos
Ordenacion
int i,j,n;
double aux,x[];
System.out.println("Ingrese la cantidad de numeros a leer:");
n= Integer.parseInt(br.readLine());
x= new double[n];
for (i=0;i System.out.println("Elemento["+i+"]:");
x[i]=Double.parseDouble(br.readLine());} for(i=1;i for(j=n-1;j>=i;j--){
if (x[j-1]>x[j]){
aux=x[j-1];
x[j-1]=x[j];
x[j]=aux;}
}
}
System.out.println("Elemento Ordenado");
for (i=0;i System.out.println("Elemento["+i+"]:"+x[i]);}
}
}
Metodo De Busqueda
int i,n,band;
double x[],elem;
System.out.println("Ingrese los numeros a leer:");
n=Integer.parseInt(br.readLine());
x=new double[n];
System.out.println("Ingrese los elementos del vector:");
for(i=0;i System.out.println("Elemento["+i+"]:");
x[i]=Double.parseDouble(br.readLine());
} System.out.println("Ingrese el elemento a buscar:");
elem=Double.parseDouble(br.readLine());
band=0;
for(i=0;i if(x[i]==elem){
System.out.println("El elemento encontrado:"+i);
band=1;
}
}
if(band==0){
System.out.println("No se encontro el elemento:");
}
}
Media Geometrica
double media[]= new double[999];
double can,sum=1,resul=0;
can=Double.parseDouble(JOptionPane.showInputDialog(null,"Ingrese Cantida De Elementos: "));
for(int i=0;i {
media[i]=Double.parseDouble(JOptionPane.showInputDialog(null,"Ingrese Datos a la Media"));
sum=sum*media[i];
} resul=Math.pow(sum, 1.0/can);
System.out.println("La Media Es Geometrica :"+resul);
} }
jueves, 8 de diciembre de 2011
miércoles, 30 de noviembre de 2011
Presentación: Búsqueda Secuencial
Definición
Está diseñada para localizar un elemento con ciertas propiedades dentro de una estructura de datos; por ejemplo, ubicar el registro correspondiente a cierta persona en una base de datos, o el mejor movimiento en una partida de ajedrez.
Utilización
Se utiliza cuando algún elemento no está ordenado o no puede ser ordenado previamente.
Consiste en buscar el elemento comparándolo secuencialmente (de ahí su nombre) con cada elemento del arreglo hasta encontrarlo, o hasta que se llegue al final.
La existencia se puede asegurar cuando el elemento es localizado, pero no podemos asegurar la no existencia hasta no haber analizado todos los elementos del arreglo
Ventajas y Desventajas
DESVENTAJA.- en un vector de N posiciones este algoritmo va a buscar posición a posición hasta dar con el dato solicitado y en el caso de que no exista pues también va a recorrer todo el arreglo.
VENTAJA.- Lo bueno de este tipo de búsqueda es que es muy sencillo de implementar.
Programa
Si tenemos un vector ya definido con los siguientes datos: ["aarona","aashta","abelarda","abelia","abigail","abril"] , todos de tipo String y queremos saber si ya existe el nombre : "Abigail" en nuestro vector entonces tenemos que hacer lo siguiente: public class BSecuencial { public static void main(String[] args) throws IOException { BufferedReader entrada = new BufferedReader (new InputStreamReader(System.in)); int encontrados=0; String [] VectorNombres = {"Aarona","Aashta","Abelarda","Abelia","Abigail ", "Abril"}; System.out.print("Digite el nombre que desea buscar: "); String nombre = entrada.readLine(); // entrada de dato a buscar for (int i=0; i
Está diseñada para localizar un elemento con ciertas propiedades dentro de una estructura de datos; por ejemplo, ubicar el registro correspondiente a cierta persona en una base de datos, o el mejor movimiento en una partida de ajedrez.
Utilización
Se utiliza cuando algún elemento no está ordenado o no puede ser ordenado previamente.
Consiste en buscar el elemento comparándolo secuencialmente (de ahí su nombre) con cada elemento del arreglo hasta encontrarlo, o hasta que se llegue al final.
La existencia se puede asegurar cuando el elemento es localizado, pero no podemos asegurar la no existencia hasta no haber analizado todos los elementos del arreglo
Ventajas y Desventajas
DESVENTAJA.- en un vector de N posiciones este algoritmo va a buscar posición a posición hasta dar con el dato solicitado y en el caso de que no exista pues también va a recorrer todo el arreglo.
VENTAJA.- Lo bueno de este tipo de búsqueda es que es muy sencillo de implementar.
Programa
Si tenemos un vector ya definido con los siguientes datos: ["aarona","aashta","abelarda","abelia","abigail","abril"] , todos de tipo String y queremos saber si ya existe el nombre : "Abigail" en nuestro vector entonces tenemos que hacer lo siguiente: public class BSecuencial { public static void main(String[] args) throws IOException { BufferedReader entrada = new BufferedReader (new InputStreamReader(System.in)); int encontrados=0; String [] VectorNombres = {"Aarona","Aashta","Abelarda","Abelia","Abigail ", "Abril"}; System.out.print("Digite el nombre que desea buscar: "); String nombre = entrada.readLine(); // entrada de dato a buscar for (int i=0; i
jueves, 10 de noviembre de 2011
Arboles
Arboles
Un árbol se define como una colección de nodos organizados en forma recursiva. Cuando hay 0 nodos se dice que el árbol esta vacío, en caso contrario el árbol consiste en un nodo denominado raíz, el cual tiene 0 o más referencias a otros árboles, conocidos como subárboles. Las raíces de los subárboles se denominan hijos de la raíz, y consecuentemente la raíz se denomina padre de las raíces de sus subárboles. Una visión gráfica de esta definición recursiva se muestra en la siguiente figura:
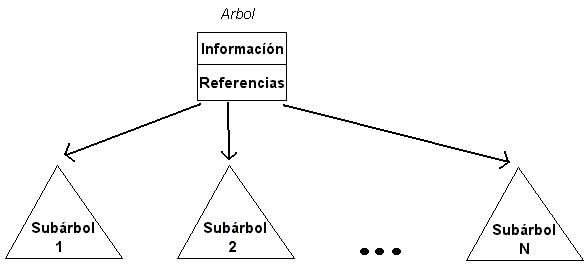
Un camino entre un nodo n1 y un nodo nk está definido como la secuencia de nodos n1, n2, ..., nk tal que ni es padre de ni+1, 1 <= i < k. El largo del camino es el número de referencias que componen el camino, que para el ejemplo son k-1. Existe un camino desde cada nodo del árbol a sí mismo y es de largo 0. Nótese que en un árbol existe un único camino desde la raíz hasta cualquier otro nodo del árbol. A partir del concepto de camino se definen los conceptos de ancestro y descendiente: un nodo n es ancestro de un nodo m si existe un camino desde n a m; un nodo n es descendiente de un nodo m si existe un camino desde m a n.
Se define la profundidad del nodo nk como el largo del camino entre la raíz del arbol y el nodo nk. Esto implica que la profundidad de la raíz es siempre 0. La altura de un nodo nk es el máximo largo de camino desde nk hasta alguna hoja. Esto implica que la altura de toda hoja es 0. La altura de un árbol es igual a la altura de la raíz, y tiene el mismo valor que la profundidad de la hoja más profunda. La altura de un árbol vacío se define como -1.
La siguiente figura muestra un ejemplo de los conceptos previamente descritos:
Tipos de Arbol
* Arbol Binario
* Arbol General
Arbol Binario
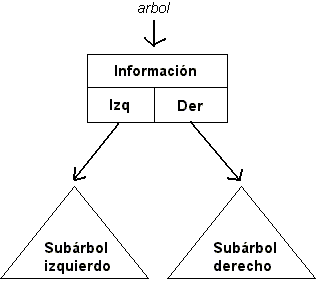
Un árbol binario es un árbol en donde cada nodo posee 2 referencias a subárboles (ni más, ni menos). En general, dichas referencias se denominan izquierda y derecha, y consecuentemente se define el subárbol izquierdo y subárbol derecho del arbol.
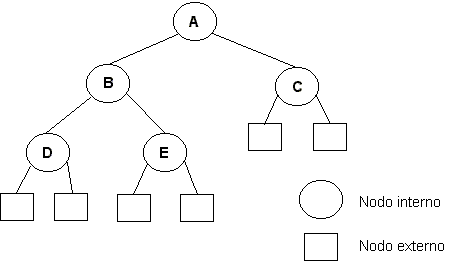
Si se define i = número de nodos internos, e = número de nodos externos, entonces se tiene que:
e = i+1
Arbol General
En un árbol general cada nodo puede poseer un número indeterminado de hijos. La implementación de los nodos en este caso se realiza de la siguiente manera: como no se sabe de antemano cuantos hijos tiene un nodo en particular se utilizan dos referencias, una a su primer hijo y otra a su hermano más cercano. La raíz del árbol necesariamente tiene la referencia a su hermano como null.
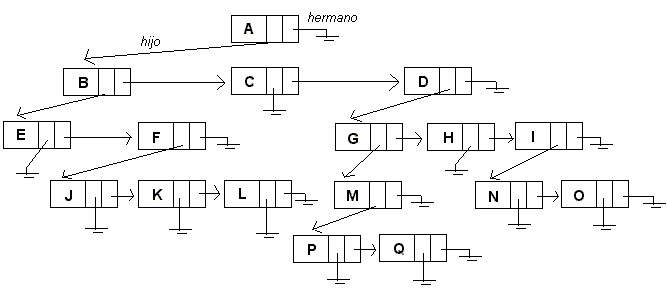
RECORRIDO DE UN ARBOL BINARIO
Si se desea manipular la información contenida en un árbol, lo primero que hay que saber es cómo se puede recorrer ese árbol, de manera que se acceda a todos los nodos del mismo solamente una vez. El recorrido completo de un árbol produce un orden lineal en la información del árbol. Este orden puede ser útil en determinadas ocasiones.
Cuando se recorre un árbol se desea tratar cada nodo y cada subárbol de la misma manera. Existen entonces seis posibles formas de recorrer un árbol binario.
(1) nodo - subárbol izquierdo - subárbol derecho
(2) subárbol izquierdo - nodo - subárbol derecho
(3) subárbol izquierdo - subárbol derecho - nodo
(4) nodo - subárbol derecho - subárbol izquierdo
(5) subárbol derecho - nodo - subárbol izquierdo
(6) subárbol derecho - subárbol izquierdo - nodo
Si se adopta el convenio de que, por razones de simetría, siempre se recorrera antes el subárbol izquierdo que el derecho, entonces tenemos solamente tres tipos de recorrido de un árbol, los tres primeros en la lista anterior. Estos recorridos, atendiendo a la posición en que se procesa la información del nodo, reciben, respectivamente, el nombre de recorrido prefijo, infijo y posfijo y dan lugar a algoritmos eminentemente recursivos.
Un árbol se define como una colección de nodos organizados en forma recursiva. Cuando hay 0 nodos se dice que el árbol esta vacío, en caso contrario el árbol consiste en un nodo denominado raíz, el cual tiene 0 o más referencias a otros árboles, conocidos como subárboles. Las raíces de los subárboles se denominan hijos de la raíz, y consecuentemente la raíz se denomina padre de las raíces de sus subárboles. Una visión gráfica de esta definición recursiva se muestra en la siguiente figura:

Un camino entre un nodo n1 y un nodo nk está definido como la secuencia de nodos n1, n2, ..., nk tal que ni es padre de ni+1, 1 <= i < k. El largo del camino es el número de referencias que componen el camino, que para el ejemplo son k-1. Existe un camino desde cada nodo del árbol a sí mismo y es de largo 0. Nótese que en un árbol existe un único camino desde la raíz hasta cualquier otro nodo del árbol. A partir del concepto de camino se definen los conceptos de ancestro y descendiente: un nodo n es ancestro de un nodo m si existe un camino desde n a m; un nodo n es descendiente de un nodo m si existe un camino desde m a n.
Se define la profundidad del nodo nk como el largo del camino entre la raíz del arbol y el nodo nk. Esto implica que la profundidad de la raíz es siempre 0. La altura de un nodo nk es el máximo largo de camino desde nk hasta alguna hoja. Esto implica que la altura de toda hoja es 0. La altura de un árbol es igual a la altura de la raíz, y tiene el mismo valor que la profundidad de la hoja más profunda. La altura de un árbol vacío se define como -1.
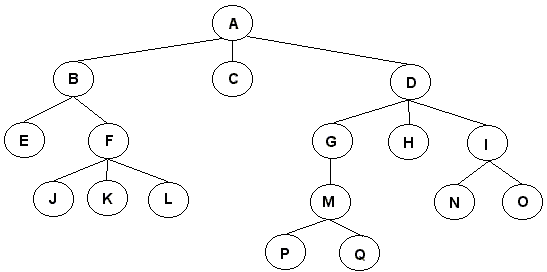
La siguiente figura muestra un ejemplo de los conceptos previamente descritos:

- A es la raíz del árbol.
- A es padre de B, C y D.
- E y F son hermanos, puesto que ambos son hijos de B.
- E, J, K, L, C, P, Q, H, N y O son las hojas del árbol.
- El camino desde A a J es único, lo conforman los nodos A-B-F-J y es de largo 3.
- D es ancestro de P, y por lo tanto P es descendiente de D.
- L no es descendiente de C, puesto que no existe un camino desde C a L.
- La profundidad de C es 1, de F es 2 y de Q es 4.
- La altura de C es 0, de F es 1 y de D es 3.
- La altura del árbol es 4 (largo del camino entre la raíz A y la hoja más profunda, P o Q).
Tipos de Arbol
* Arbol Binario
* Arbol General
Arbol Binario
Un árbol binario es un árbol en donde cada nodo posee 2 referencias a subárboles (ni más, ni menos). En general, dichas referencias se denominan izquierda y derecha, y consecuentemente se define el subárbol izquierdo y subárbol derecho del arbol.

class NodoArbolBinario
{
Object elemento;
NodoArbolBinario izq;
NodoArbolBinario der;
}
Los nodos en sí que conforman un árbol binario se denominan nodos internos, y todas las referencias que son null se denominan nodos externos. 
Propiedades de los árboles binarios
Propiedad 1:Si se define i = número de nodos internos, e = número de nodos externos, entonces se tiene que:
Arbol General
En un árbol general cada nodo puede poseer un número indeterminado de hijos. La implementación de los nodos en este caso se realiza de la siguiente manera: como no se sabe de antemano cuantos hijos tiene un nodo en particular se utilizan dos referencias, una a su primer hijo y otra a su hermano más cercano. La raíz del árbol necesariamente tiene la referencia a su hermano como null.
class NodoArbolGeneral
{
Object elemento;
NodoArbolGeneral hijo;
NodoArbolGeneral hermano;
}

Programa utilizando Arboles
public class Ejemplo {
public static void main(String[] args) {
Arbol arbol = null;
arbol = Arbol.insertar( arbol, new Integer(5));
arbol = Arbol.insertar( arbol, new Integer(2));
arbol = Arbol.insertar( arbol, new Integer(6));
arbol = Arbol.insertar( arbol, new Integer(1));
arbol = Arbol.insertar( arbol, new Integer(3));
arbol = Arbol.insertar( arbol, new Integer(4));
IAccion accion = new AccionAdapter(){
public void accion(Object dato) {
System.out.println(dato);
}
};
System.out.println( "\nListado Pre-Orden\n");
Arbol.inorden( arbol, accion );
System.out.println( "\nListado In-Orden\n");
Arbol.inorden( arbol, accion );
System.out.println( "\nListado Post-Orden\n");
Arbol.inorden( arbol, accion );
Arbol palabras = null;
palabras = Arbol.insertar( palabras, "San Luis Potosí");
palabras = Arbol.insertar( palabras, "Durango");
palabras = Arbol.insertar( palabras, "Coahuila");
palabras = Arbol.insertar( palabras, "Jalisco");
palabras = Arbol.insertar( palabras, "Aguascalientes");
palabras = Arbol.insertar( palabras, "Guanajuato");
System.out.println( "\nListado Pre-Orden\n");
Arbol.inorden(palabras, accion );
System.out.println( "\nListado In-Orden\n");
Arbol.inorden(palabras, accion );
System.out.println( "\nListado Post-Orden\n");
Arbol.inorden( palabras, accion );
}
}
public static void main(String[] args) {
Arbol arbol = null;
arbol = Arbol.insertar( arbol, new Integer(5));
arbol = Arbol.insertar( arbol, new Integer(2));
arbol = Arbol.insertar( arbol, new Integer(6));
arbol = Arbol.insertar( arbol, new Integer(1));
arbol = Arbol.insertar( arbol, new Integer(3));
arbol = Arbol.insertar( arbol, new Integer(4));
IAccion accion = new AccionAdapter(){
public void accion(Object dato) {
System.out.println(dato);
}
};
System.out.println( "\nListado Pre-Orden\n");
Arbol.inorden( arbol, accion );
System.out.println( "\nListado In-Orden\n");
Arbol.inorden( arbol, accion );
System.out.println( "\nListado Post-Orden\n");
Arbol.inorden( arbol, accion );
Arbol palabras = null;
palabras = Arbol.insertar( palabras, "San Luis Potosí");
palabras = Arbol.insertar( palabras, "Durango");
palabras = Arbol.insertar( palabras, "Coahuila");
palabras = Arbol.insertar( palabras, "Jalisco");
palabras = Arbol.insertar( palabras, "Aguascalientes");
palabras = Arbol.insertar( palabras, "Guanajuato");
System.out.println( "\nListado Pre-Orden\n");
Arbol.inorden(palabras, accion );
System.out.println( "\nListado In-Orden\n");
Arbol.inorden(palabras, accion );
System.out.println( "\nListado Post-Orden\n");
Arbol.inorden( palabras, accion );
}
}
Video. Aplicacion Arboles en Java
Recorrido de un Arbol Binario
Si se desea manipular la información contenida en un árbol, lo primero que hay que saber es cómo se puede recorrer ese árbol, de manera que se acceda a todos los nodos del mismo solamente una vez. El recorrido completo de un árbol produce un orden lineal en la información del árbol. Este orden puede ser útil en determinadas ocasiones.
Cuando se recorre un árbol se desea tratar cada nodo y cada subárbol de la misma manera. Existen entonces seis posibles formas de recorrer un árbol binario.
(1) nodo - subárbol izquierdo - subárbol derecho
(2) subárbol izquierdo - nodo - subárbol derecho
(3) subárbol izquierdo - subárbol derecho - nodo
(4) nodo - subárbol derecho - subárbol izquierdo
(5) subárbol derecho - nodo - subárbol izquierdo
(6) subárbol derecho - subárbol izquierdo - nodo
Si se adopta el convenio de que, por razones de simetría, siempre se recorrera antes el subárbol izquierdo que el derecho, entonces tenemos solamente tres tipos de recorrido de un árbol, los tres primeros en la lista anterior. Estos recorridos, atendiendo a la posición en que se procesa la información del nodo, reciben, respectivamente, el nombre de recorrido prefijo, infijo y posfijo y dan lugar a algoritmos eminentemente recursivos.
Grafos
Un grafo en el ámbito de las ciencias de la computación es una estructura de datos, en concreto un tipo abstracto de datos (TAD), que consiste en un conjunto de nodos (también llamados vértices) y un conjunto de arcos (aristas) que establecen relaciones entre los nodos. El concepto de grafo TAD desciende directamente del concepto matemático de grafo.
Informalmente se define como G = (V, E), siendo los elementos de V los vértices, y los elementos de E, las aristas (edges en inglés). Formalmente, un grafo, G, se define como un par ordenado, G = (V, E), donde V es un conjunto finito y E es un conjunto que consta de dos elementos de V.
Un grafo en el ámbito de las ciencias de la computación es una estructura de datos, en concreto un tipo abstracto de datos (TAD), que consiste en un conjunto de nodos (también llamados vértices) y un conjunto de arcos (aristas) que establecen relaciones entre los nodos. El concepto de grafo TAD desciende directamente del concepto matemático de grafo.
Informalmente se define como G = (V, E), siendo los elementos de V los vértices, y los elementos de E, las aristas (edges en inglés). Formalmente, un grafo, G, se define como un par ordenado, G = (V, E), donde V es un conjunto finito y E es un conjunto que consta de dos elementos de V.
martes, 1 de noviembre de 2011
Colas
Una cola es una estructura de datos, caracterizada por ser una secuencia de elementos en la que la operación de inserciónpush se realiza por un extremo y la operación de extracción pop por el otro. También se le llama estructura FIFO (del inglés First In First Out), debido a que el primer elemento en entrar será también el primero en salir.
Las colas se utilizan en sistemas informáticos, transportes y operaciones de investigación (entre otros), dónde los objetos, personas o eventos son tomados como datos que se almacenan y se guardan mediante colas para su posterior procesamiento. Este tipo de estructura de datos abstracta se implementa en lenguajes orientados a objetos mediante clases, en forma de listas enlazadas.
Uso
La particularidad de una estructura de datos de cola es el hecho de que sólo podemos acceder al primer y al último elemento de la estructura. Así mismo, los elementos sólo se pueden eliminar por el principio y sólo se pueden añadir por el final de la cola,
Operaciones con Colas
- Crear: se crea la cola vacía.
- Encolar (añadir, entrar, insertar): se añade un elemento a la cola. Se añade al final de esta.
- Desencolar (sacar, salir, eliminar): se elimina el elemento frontal de la cola, es decir, el primer elemento que entró.
- Frente (consultar, front): se devuelve el elemento frontal de la cola, es decir, el primer elemento que entró.

Ejemplos de colas en la vida real serían: personas comprando en un supermercado, esperando para entrar a ver un partido de béisbol, esperando en el cine para ver una película, una pequeña peluquería, etc. La idea esencial es que son todos líneas de espera.
Ejemplo Cola.Java
public void inserta(Elemento x) {
Nodo Nuevo;
Nuevo = new Nodo(x, null);
if (NodoCabeza == null) {
NodoCabeza = Nuevo;
} else {
NodoFinal.Siguiente = Nuevo;
}
NodoFinal = Nuevo;
}
public Elemento cabeza() throws IllegalArgumentException {
if (NodoCabeza == null) {
throw new IllegalArgumentException();
} else {
return NodoCabeza.Info;
}
}
public Cola() {
// Devuelve una Cola vacía
NodoCabeza = null;
NodoFinal = null;
}
Tipos de Colas
- Colas circulares (anillos): en las que el último elemento y el primero están unidos.
- Colas de prioridad: En ellas, los elementos se atienden en el orden indicado por una prioridad asociada a cada uno. Si varios elementos tienen la misma prioridad, se atenderán de modo convencional según la posición que ocupen. Hay 2 formas de implementación:
- Añadir un campo a cada nodo con su prioridad. Resulta conveniente mantener la cola ordenada por orden de prioridad.
- Crear tantas colas como prioridades haya, y almacenar cada elemento en su cola.
- Bicolas: son colas en donde los nodos se pueden añadir y quitar por ambos extremos; se les llama DEQUE (Double Ended QUEue). Para representar las bicolas lo podemos hacer con un array circular con Inicio y Fin que apunten a cada uno de los extremos. Hay variantes:
- Bicolas de entrada restringida: Son aquellas donde la inserción sólo se hace por el final, aunque podemos eliminar al inicio ó al final.
- Bicolas de salida restringida: Son aquellas donde sólo se elimina por el final, aunque se puede insertar al inicio y al final.
Video con Colas en Java
Recursividad
La recursividad es una función que se llama a sí misma para dividir un problema en problemas más sencillos, el método recursivo debe estar compuesto de una caso base para el cual ya se conoce un resultado y una llamada al mismo método con una versión ligeramente más sencilla del problema inicial
ejemplo 1, factoriales:
Para todo n entero natural, se llama factorial n (n!) al producto de todos los enteros entre 1 y n:
| n | n! | ||
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 2 × 1 | = 2 × 1! | = 2 |
| 3 | 3 × 2 × 1 | = 3 × 2! | = 6 |
| 4 | 4 × 3 × 2 × 1 | = 4 × 3! | = 24 |
| 5 | 5 × 4 × 3 × 2 × 1 | = 5 × 4! | = 120 |
| 6 | etc | etc |
Código:
1 2 3 4 5 6 | public void factoriales(long n){ if(n==1) return 1; else return n*factoriales(n-1);} |
El método factoriales se llama a sí mismo disminuyendo cada vez el numero inicial en una unidad hasta que llega a valer 1 y por lo tanto alcanza el caso base, en ese momento se devuelven todas las llamadas recursivas realizas al método factoriales retornando el valor del actual multiplicado por el valor anterior.
ejemplo 2, Fibonachi:
La sucesion de Fibonachi comienza por 0 y 1, y cada numero siguiente es la
suma de los dos anteriores:
0,1,1,2,3,5,8,13,21,34,55,89
Código:
1 2 3 4 5 6 7 | public void fibonachi(long n){ if(n==0 || n==1) return n; else return fibonachi(n-2)+fibonachi(n-1);} |
Este método esta compuesto de dos casos bases, y de dos llamadas recursivas al método, a esto se le denomina recursividad mútliple, a diferencia del método factoriales que sólo hace una llamada recursiva y se denomina recursividad simple. En ambos casos es de tipo directa, también es posible efectuar recursión indirectamente: una método puede llamar a otro quien, a su vez, acabe llamando al primero.
A continuación se expone un ejemplo de programa que utiliza recursión indirecta, y nos dice si un número es par o impar. Al igual que el programa anterior, hay otro método mucho más sencillo de determinar si un número es par o impar, basta con determinar el resto de la división entre dos. Por ejemplo: si hacemos par(2) devuelve 1 (cierto). Si hacemos impar(4) devuelve 0 (falso).
Código:
1 2 3 4 5 6 7 8 9 10 11 | int par(int n){ if (n == 0) return 1; return impar(n-1);}int impar(int n){ if (n == 0) return 0; return par(n-1);} |
Código:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | int x[]={7,3,4,6,8,9,5}; int n = 7; // Enviamos datos max(n, x); public static int max(int n, int x[]) { if(n == 1) return x[0]; if (x[n-1] > max(n-1, x)) return x[n-1]; else return max(n-1, x); } |
Hay que apuntar que el factorial puede obtenerse con facilidad sin necesidad de emplear funciones recursivas, es más, el uso del programa anterior es muy ineficiente, pero es un ejemplo muy claro.
Dado un array constituido de números enteros, devolver la suma de todos los elementos. En este caso se desconoce el número de elementos. En cualquier caso se garantiza que el último elemento del array es -1, número que no aparecerá en ninguna otra posición.
Código:
1 2 3 4 5 6 7 8 9 | private static int sumaArray2(int vector[], int n){ if(n==-1)return 0; else return vector[n]+ sumaArray2(vector, n-1); }static int []array={1,2,3,4,5,6};System.out.println(sumaArray2(array,array.length-1)); |
Dado un array constituido de números enteros y que contiene N elementos siendo N >= 1, devolver el elemento mayor.
Código:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | static int []array={510,41,300,4,25,6}; private static int mayor(int vector[], int n){ int aux; if(n==-1)return 0; else{ aux = mayor(vector, n-1); if(vector[n]>aux) return vector[n]; else return aux; } } System.out.println(mayor(array,array.length-1)); |
máximo comun divisor.
Código:
1 2 3 4 5 6 7 8 9 10 | private static long mcd(long a, long b){ if(b==0) return a; else return mcd(b,a%b); } System.out.println(mcd(80,25));resultado 5; |
Video utilizando Recursividad
Suscribirse a:
Comentarios (Atom)