Arboles

Arboles
Un árbol se define como una colección de nodos organizados en forma recursiva. Cuando hay 0 nodos se dice que el árbol esta vacío, en caso contrario el árbol consiste en un nodo denominado raíz, el cual tiene 0 o más referencias a otros árboles, conocidos como subárboles. Las raíces de los subárboles se denominan hijos de la raíz, y consecuentemente la raíz se denomina padre de las raíces de sus subárboles. Una visión gráfica de esta definición recursiva se muestra en la siguiente figura:


Los nodos que no poseen hijos se denominan hojas. Dos nodos que tienen el padre en común se denominan hermanos.
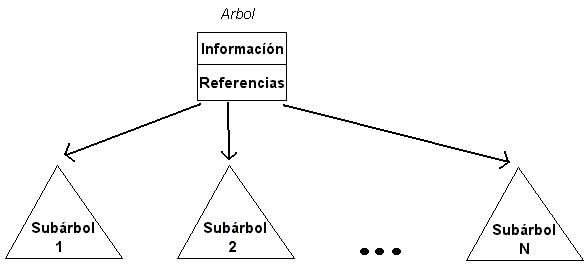
Un camino entre un nodo n₁ y un nodo n_k está definido como la secuencia de nodos n₁, n₂, ..., n_k tal que n_i es padre de n_i+1, 1 <= i < k. El largo del camino es el número de referencias que componen el camino, que para el ejemplo son k-1. Existe un camino desde cada nodo del árbol a sí mismo y es de largo 0. Nótese que en un árbol existe un único camino desde la raíz hasta cualquier otro nodo del árbol. A partir del concepto de camino se definen los conceptos de ancestro y descendiente: un nodo n es ancestro de un nodo m si existe un camino desde n a m; un nodo n es descendiente de un nodo m si existe un camino desde m a n.
Se define la profundidad del nodo n_k como el largo del camino entre la raíz del arbol y el nodo n_k. Esto implica que la profundidad de la raíz es siempre 0. La altura de un nodo n_k es el máximo largo de camino desde n_k hasta alguna hoja. Esto implica que la altura de toda hoja es 0. La altura de un árbol es igual a la altura de la raíz, y tiene el mismo valor que la profundidad de la hoja más profunda. La altura de un árbol vacío se define como -1.
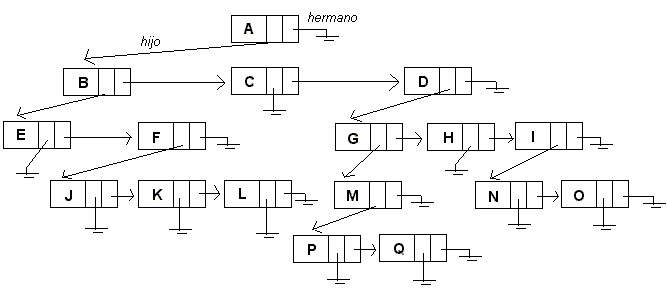
La siguiente figura muestra un ejemplo de los conceptos previamente descritos:

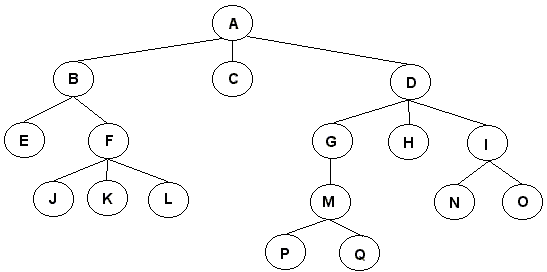
• A es la raíz del árbol.
• A es padre de B, C y D.
• E y F son hermanos, puesto que ambos son hijos de B.
• E, J, K, L, C, P, Q, H, N y O son las hojas del árbol.
• El camino desde A a J es único, lo conforman los nodos A-B-F-J y es de largo 3.
• D es ancestro de P, y por lo tanto P es descendiente de D.
• L no es descendiente de C, puesto que no existe un camino desde C a L.
• La profundidad de C es 1, de F es 2 y de Q es 4.
• La altura de C es 0, de F es 1 y de D es 3.
• La altura del árbol es 4 (largo del camino entre la raíz A y la hoja más profunda, P o Q).

Tipos de Arbol
* Arbol Binario
* Arbol General

Arbol Binario
Un árbol binario es un árbol en donde cada nodo posee 2 referencias a subárboles (ni más, ni menos). En general, dichas referencias se denominan izquierda y derecha, y consecuentemente se define el subárbol izquierdo y subárbol derecho del arbol.


En este caso, la implementacion del nodo de un árbol binario es como sigue:

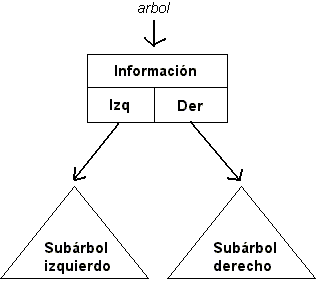
class NodoArbolBinario
{
  Object elemento;
  NodoArbolBinario izq;
  NodoArbolBinario der;
}

Los nodos en sí que conforman un árbol binario se denominan nodos internos, y todas las referencias que son null se denominan nodos externos.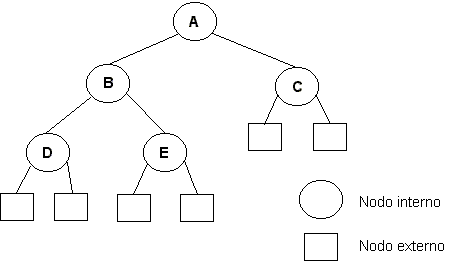

Propiedades de los árboles binarios

Propiedad 1:
Si se define i = número de nodos internos, e = número de nodos externos, entonces se tiene que:


e = i+1

Arbol General
En un árbol general cada nodo puede poseer un número indeterminado de hijos. La implementación de los nodos en este caso se realiza de la siguiente manera: como no se sabe de antemano cuantos hijos tiene un nodo en particular se utilizan dos referencias, una a su primer hijo y otra a su hermano más cercano. La raíz del árbol necesariamente tiene la referencia a su hermano como null.

class NodoArbolGeneral
{
  Object elemento;
  NodoArbolGeneral hijo;
  NodoArbolGeneral hermano;
}

Nótese que todo árbol general puede representarse como un árbol binario, con la salvedad que el hijo derecho de la raíz es siempre null. Si se permite que la raíz del árbol tenga hermanos, lo que se conoce como bosque, entonces se tiene que el conjunto de los bosques generales es isomorfo al conjunto de los árboles binarios. En efecto, las propiedades vistas en los árboles binarios se siguen cumpliendo en los árboles generales.

Programa utilizando Arboles

public class Ejemplo {
public static void main(String[] args) {
Arbol arbol = null;
arbol = Arbol.insertar( arbol, new Integer(5));
arbol = Arbol.insertar( arbol, new Integer(2));
arbol = Arbol.insertar( arbol, new Integer(6));
arbol = Arbol.insertar( arbol, new Integer(1));
arbol = Arbol.insertar( arbol, new Integer(3));
arbol = Arbol.insertar( arbol, new Integer(4));
IAccion accion = new AccionAdapter(){
public void accion(Object dato) {
System.out.println(dato);
}
};
System.out.println( "\nListado Pre-Orden\n");
Arbol.inorden( arbol, accion );
System.out.println( "\nListado In-Orden\n");
Arbol.inorden( arbol, accion );
System.out.println( "\nListado Post-Orden\n");
Arbol.inorden( arbol, accion );
Arbol palabras = null;
palabras = Arbol.insertar( palabras, "San Luis Potosí");
palabras = Arbol.insertar( palabras, "Durango");
palabras = Arbol.insertar( palabras, "Coahuila");
palabras = Arbol.insertar( palabras, "Jalisco");
palabras = Arbol.insertar( palabras, "Aguascalientes");
palabras = Arbol.insertar( palabras, "Guanajuato");
System.out.println( "\nListado Pre-Orden\n");
Arbol.inorden(palabras, accion );
System.out.println( "\nListado In-Orden\n");
Arbol.inorden(palabras, accion );
System.out.println( "\nListado Post-Orden\n");
Arbol.inorden( palabras, accion );
}
}

Video. Aplicacion Arboles en Java

Arboles utilizando Java

Recorrido de un Arbol Binario

RECORRIDO DE UN ARBOL BINARIO
Si se desea manipular la información contenida en un árbol, lo primero que hay que saber es cómo se puede recorrer ese árbol, de manera que se acceda a todos los nodos del mismo solamente una vez. El recorrido completo de un árbol produce un orden lineal en la información del árbol. Este orden puede ser útil en determinadas ocasiones.

Cuando se recorre un árbol se desea tratar cada nodo y cada subárbol de la misma manera. Existen entonces seis posibles formas de recorrer un árbol binario.

(1) nodo - subárbol izquierdo - subárbol derecho

(2) subárbol izquierdo - nodo - subárbol derecho

(3) subárbol izquierdo - subárbol derecho - nodo

(4) nodo - subárbol derecho - subárbol izquierdo

(5) subárbol derecho - nodo - subárbol izquierdo

(6) subárbol derecho - subárbol izquierdo - nodo

Si se adopta el convenio de que, por razones de simetría, siempre se recorrera antes el subárbol izquierdo que el derecho, entonces tenemos solamente tres tipos de recorrido de un árbol, los tres primeros en la lista anterior. Estos recorridos, atendiendo a la posición en que se procesa la información del nodo, reciben, respectivamente, el nombre de recorrido prefijo, infijo y posfijo y dan lugar a algoritmos eminentemente recursivos.

Grafos



Un grafo en el ámbito de las ciencias de la computación es una estructura de datos, en concreto un tipo abstracto de datos (TAD), que consiste en un conjunto de nodos (también llamados vértices) y un conjunto de arcos (aristas) que establecen relaciones entre los nodos. El concepto de grafo TAD desciende directamente del concepto matemático de grafo.

Informalmente se define como G = (V, E), siendo los elementos de V los vértices, y los elementos de E, las aristas (edges en inglés). Formalmente, un grafo, G, se define como un par ordenado, G = (V, E), donde V es un conjunto finito y E es un conjunto que consta de dos elementos de V.